CUADRILÁTERO
Para el núcleo conspirativo que participó en el golpe de Estado de Primo de Rivera de 1923, véase Cuadrilátero (Dictadura de Primo de Rivera).
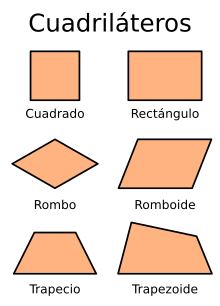
Clases de cuadriláteros convexos.
La palabra "cuadrilátero" procede de dos palabras latinas quadri, que significa cuatro, y latus, que significa lado.
Los cuadriláteros según su forma se dividen en complejos y simples, y estos a su vez se dividen en cóncavos y convexos, y estos a su vez pueden estar o no inscritos o circunscritos.






 vértices donde {\displaystyle n}
vértices donde {\displaystyle n} es el número de vértices de la base.
es el número de vértices de la base.
 y {\displaystyle r_{2}\,}
y {\displaystyle r_{2}\,} , la
, la  , y la
, y la  , entre las cuales se cumple la relación del
, entre las cuales se cumple la relación del 
