CUADRILÁTERO
Para el núcleo conspirativo que participó en el golpe de Estado de Primo de Rivera de 1923, véase Cuadrilátero (Dictadura de Primo de Rivera).
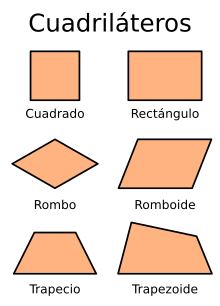
Clases de cuadriláteros convexos.
La palabra "cuadrilátero" procede de dos palabras latinas quadri, que significa cuatro, y latus, que significa lado.
Los cuadriláteros según su forma se dividen en complejos y simples, y estos a su vez se dividen en cóncavos y convexos, y estos a su vez pueden estar o no inscritos o circunscritos.
Propiedades
Los cuadriláteros tienen dos diagonales.
Las diagonales de un cuadrilátero se cortan si y solamente si es convexo.
La suma de la medida de los ángulos de un cuadrilátero {\displaystyle ABCD}
convexo es 360º o 2π radianes.{\displaystyle \angle A+\angle B+\angle C+\angle D=360^{\circ }}
convexo es 360º o 2π radianes.{\displaystyle \angle A+\angle B+\angle C+\angle D=360^{\circ }}
Todo cuadrilátero simple puede expresarse como la unión de dos triángulos con lado común que es una de las diagonales.
En un cuadrilátero inscrito en una circunferencia la suma de la medida de sus ángulos opuestos es igual a 180º.
Sea ABCD un cuadrilátero inscrito en una circunferencia de diámetro {\displaystyle AB}
, entonces las proyecciones de los lados AD y BC sobre la recta CD son iguales.1
, entonces las proyecciones de los lados AD y BC sobre la recta CD son iguales.1
El área de un cuadrilátero inscrito se obtiene con la fórmula {\displaystyle A={\sqrt {(p-a)(p-b)(p-c)(p-d)}}}
donde a, b, c, d son los lados y p es el semiperímetro.
donde a, b, c, d son los lados y p es el semiperímetro.
Si 2α es la suma de dos ángulos opuestos de un cuadrilátero circunscrito, A su área, a,b, c, d sus lados entonces cabe la fórmula A2 = (abcd)sen2α.2
Si las diagonales de un cuadrilátero convexo lo divide en cuatro triángulos y los radios de la circunferencias inscritas en estos triángulos son iguales, entonces dicho cuadrilátero es un rombo.
Si se unen con cuatro segmentos los puntos medios de todos los lados de un cuadrilátero, entonces dichos segmentos forman un paralelogramo.
Si en el cuadrilátero ABCD los radios de las circunferencias inscritas en los triángulos ABC, BCD, CDA, DAB son iguales, entonces dicho cuadrilátero es un rectángulo.
Si las diagonales de un cuadrilátero lo dividen en cuatro triángulos de igual perímetro, entonces el cuadrilátero original es un rombo.3
Si un cuadrilátero está circunscrito entonces la suma de sus lados opuestos con iguales. {\displaystyle AB+CD=BC+DA}
.4
.4
Para un cuadrilátero convexo se cumple {\displaystyle a^{2}+b^{2}+c^{2}+d^{2}=d_{1}^{2}+d_{2}^{2}+4m^{2}}
donde {\displaystyle a,b,c,d}
son los lados; {\displaystyle d_{1},d_{2}}
,las diagonales y m, la longitud del segmento que une los puntos medios de las diagonales.
donde {\displaystyle a,b,c,d} son los lados; {\displaystyle d_{1},d_{2}},las diagonales y m, la longitud del segmento que une los puntos medios de las diagonales.
donde {\displaystyle d_{1},d_{2}} son las diagonales y {\displaystyle m_{1},m_{2}}
son los segmentos que unen los puntos medios de lados opuestos.
Elementos de un cuadrilátero
- Los elementos de un cuadrilátero son los siguientes:
- 4 vértices: puntos de intersección de los lados que conforman el cuadrilátero.
- 4 lados: segmentos que unen los vértices contiguos.
- 2 diagonales: segmentos cuyos extremos son dos vértices no contiguos.
- 4 ángulos interiores: el determinado por dos lados contiguos.
- 4 ángulos exteriores: el determinado por la prolongación de uno de los lados sobre un vértice y el contiguo en el mismo vértice.
Deltoides
Tipos de Paralelogramos
Los cuadriláteros se clasifican según el paralelismo de sus lados, sus longitudes y sus ángulos interiores:
Paralelogramo: sus lados opuestos son paralelos.
Cuadrado: todos sus lados son iguales, todos sus ángulos interiores son rectos, sus diagonales son iguales y perpendiculares entre si, tiene una circunferencia inscritas y otra circunscrita.
Rombo: todos sus lados son iguales, cada par de ángulos agudos y obtusos son opuestos, sus diagonales son distintas y perpendiculares entre sí, son bisectrices, tiene una circunferencia inscrita.
Rectángulo: sus lados opuestos son iguales dos a dos y los paralelos, todos sus ángulos interiores son rectos, sus dos diagonales son iguales pero no son perpendiculares entre si y tiene una circunferencia circunscrita.
Romboide: sus lados opuestos son iguales dos a dos, cada par de ángulos agudos y obtusos son opuestos, sus dos diagonales son de distinta longitud y no son perpendiculares entre sí.
Trapecios: En geometría, se llama trapecio a un cuadrilátero que tiene dos lados no consecutivos paralelos llamados bases del trapecio, y el segmento perpendicular entre las dos bases y su propia longitud son llamadas altura del trapecio
Trapezoides: En geometría euclídea plana, un trapezoide es un cuadrilátero convexo sin lados paralelos.
Taxonomía de los cuadriláteros[editar]
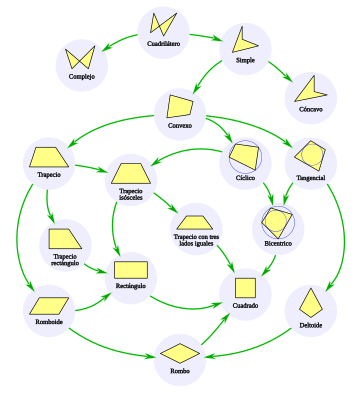
En el gráfico ilustrativo de la taxonomía de los cuadriláteros se pasa de las definiciones más generales a las más específicas siguiendo el sentido de las flechas.
Así se parte de un cuadrilátero definido como un polígono cerrado de cuatro lados, sin más restricciones, para diferenciar los cuadriláteros compuestos de los simples.
En un cuadrilátero complejo, dos de sus lados se cortan. En uno simple los lados no se cruzan.
Los cuadriláteros simples se dividen en:
Cóncavos. En un cuadrilátero cóncavo al menos uno de sus ángulos interiores mide más de 180°.
Convexos. Un cuadrilátero convexo no tiene ángulos interiores que midan más de 180°. Los convexos se subdividen en:
Cuadrilátero cíclico, si se puede trazar una circunferencia que pase por sus vértices.
Trapecios, si tienen dos lados paralelos. Se diferencian:
Romboide, como caso más general de paralelogramo, si los lados son paralelos dos a dos.
Trapecio isósceles, cuyos lados no paralelos son de igual medida. Este trapecio también es cíclico.
A un cuadrilátero que al mismo tiempo sea cíclico y tangencial se le denomina cuadrilátero bicéntrico. El deltoide es tangencial con dos pares de lados iguales.
Un caso particular de trapecio isósceles es cuando la longitud de una de las bases es igual que la de sus lados, por lo cual se configura un trapecio de tres lados iguales.
Cuadrilátero simétrico[editar]
Se llama así cualquier cuadrilátero en el cual una de sus diagonales sirve de eje de simetría. Por ejemplo: el rombo, el deltoide, el cuadrado.
El rectángulo es un cuadrilátero que simultáneamente cumple las características de:
Paralelogramo, al ser paralelos sus lados opuestos.
Trapecio rectángulo, porque los lados son perpendiculares a las bases.
Trapecio isósceles, por ser de igual longitud los lados que no constituyen las bases.
Del mismo modo se puede verificar que el rombo es un deltoide paralelogramo, pues cumple las características de ambos.
Por último, el cuadrado puede considerarse rombo, rectángulo, con lados iguales y bicéntrico.
Fórmulas
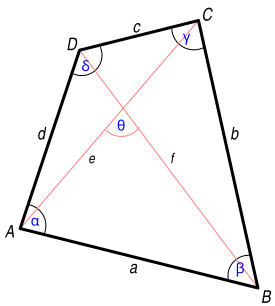
Los cuatro lados de un cuadrilátero: a, b, c, d ;
los cuatro vértices: A, B, C, D ;
las dos diagonales: e, f.
La suma de los ángulos internos es igual a 360°:{\displaystyle \alpha +\beta +\gamma +\delta =360^{\circ }}
Si las diagonales son perpendiculares, ocurre la relación siguiente:{\displaystyle \theta =90^{\circ }\Longleftrightarrow a^{2}+c^{2}=b^{2}+d^{2}}
El área de un cuadrilátero se puede calcular mediante cualquiera de estas seis fórmulas:{\displaystyle A={\frac {ef\sin \theta }{2}}}
{\displaystyle A={\frac {ad\sin \alpha +bc\sin \gamma }{2}}={\frac {ab\sin \beta +cd\sin \delta }{2}}}
{\displaystyle A={\frac {1}{4}}\left(b^{2}+d^{2}-a^{2}-c^{2}\right)\tan \theta }
{\displaystyle A={\frac {1}{4}}{\sqrt {4e^{2}f^{2}-\left(b^{2}+d^{2}-a^{2}-c^{2}\right)^{2}}}}
{\displaystyle A={\frac {1}{2}}{\sqrt {|{\vec {e}}|^{2}|{\vec {f}}|^{2}-({\vec {e}}\cdot {\vec {f}})^{2}}}}
{\displaystyle A={\frac {ad\sin \alpha +bc\sin \gamma }{2}}={\frac {ab\sin \beta +cd\sin \delta }{2}}}{\displaystyle A={\frac {1}{4}}\left(b^{2}+d^{2}-a^{2}-c^{2}\right)\tan \theta }{\displaystyle A={\frac {1}{4}}{\sqrt {4e^{2}f^{2}-\left(b^{2}+d^{2}-a^{2}-c^{2}\right)^{2}}}}{\displaystyle A={\frac {1}{2}}{\sqrt {|{\vec {e}}|^{2}|{\vec {f}}|^{2}-({\vec {e}}\cdot {\vec {f}})^{2}}}}
{\displaystyle A={\tfrac {1}{2}}ad\cdot \sin {\alpha }+{\tfrac {1}{4}}{\sqrt {4b^{2}c^{2}-(b^{2}+c^{2}-a^{2}-d^{2}+2ad\cdot \cos {\alpha })^{2}}}}
(para un cuadrilátero con concavidad en C cambiar el primer signo + por -).
(para un cuadrilátero con concavidad en C cambiar el primer signo + por -).
Cuadriláteros inscriptos[editar]
Son aquellos cuyos vértices están en una circunferencia y sus lados son cuerdas. Se establecen las siguientes fórmulas siendo
sus lados a,b,c d; y sus diagonales d1, d2
{\displaystyle d_{1}d_{2}=ac+bd}
{\displaystyle {\frac {d_{1}}{d_{2}}}={\frac {ad+bc}{ab+cd}}}
{\displaystyle d_{1}={\sqrt {\frac {(ad+bc)(ac+bd)}{ab+cd}}}}
{\displaystyle d_{2}={\sqrt {\frac {(ab+cd)(ac+bd)}{ad+bc}}}}
No hay comentarios:
Publicar un comentario